Calcul de la Masse Critique d’Uranium-235
Comprendre le Calcul de la Masse Critique d’Uranium-235
Dans un réacteur nucléaire de recherche, on utilise de l’uranium enrichi pour obtenir une réaction en chaîne soutenue. L’uranium naturel contient environ 0,7% d’uranium-235 et 99,3% d’uranium-238.
Pour cet exercice, supposons que l’uranium a été enrichi pour contenir 5% d’uranium-235. La masse critique de l’uranium-235, qui est la quantité nécessaire pour maintenir une réaction en chaîne autosuffisante, dépend de plusieurs facteurs, notamment de la forme et de la densité du matériau, ainsi que de la présence de matières réfléchissantes (comme l’eau lourde) qui peuvent ralentir les neutrons.
Données:
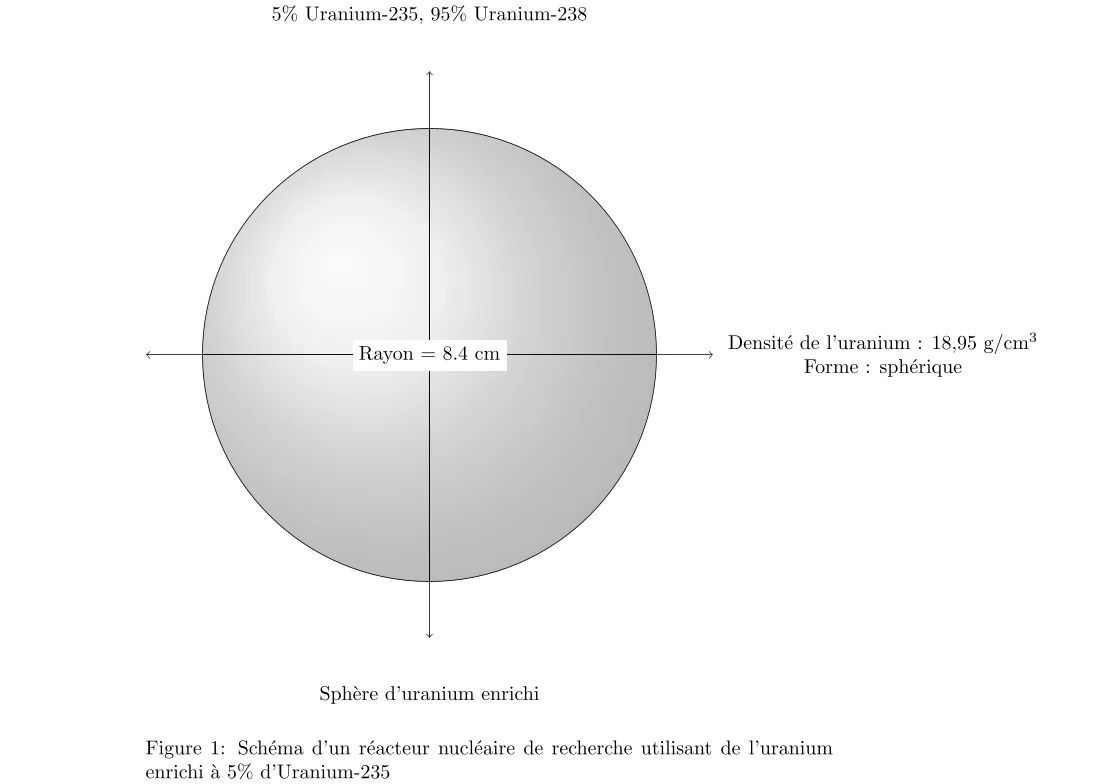
- Enrichissement de l’uranium : 5% d’uranium-235
- Densité de l’uranium : 18,95 g/cm³
- Forme de l’uranium : sphérique
- Rayon de la sphère d’uranium nécessaire pour atteindre la masse critique sans réflecteur de neutrons : 8,4 cm
Question:
Calculer la masse totale d’uranium enrichi nécessaire pour atteindre la masse critique en considérant les données fournies.
Correction : Calcul de la Masse Critique d’Uranium-235
1. Calcul du volume de la sphère d’uranium
Le volume d’une sphère se calcule à partir de son rayon en utilisant la formule du volume pour une forme sphérique.
Formule :
\[ V = \frac{4}{3} \pi r^3 \]
Données :
- \(r = 8,4 \, \text{cm}\)
Calcul :
\[ V = \frac{4}{3} \pi (8,4 \, \text{cm})^3 \] \[ V = \frac{4}{3} \pi \times 592,704 \, \text{cm}^3 \] \[ V = 2483,48 \, \text{cm}^3 \]
2. Calcul de la masse totale de l’uranium enrichi
La masse peut être calculée en multipliant le volume de la substance par sa densité.
Formule :
\[ \text{Masse} = \text{densité} \times \text{volume} \]
Données :
- \(\text{Densité} = 18,95 \, \text{g/cm}^3\)
- \(\text{Volume} = 2483,48 \, \text{cm}^3\)
Calcul :
\[ \text{Masse} = 18,95 \, \text{g/cm}^3 \times 2483,48 \, \text{cm}^3 \] \[ \text{Masse} = 47040,83 \, \text{g} \]
3. Calcul de la masse d’uranium-235 dans la sphère enrichie
Pour déterminer la quantité d’uranium-235 dans l’uranium enrichi, multipliez la masse totale d’uranium par le pourcentage d’uranium-235.
Formule :
\[ Masse_{\text{U-235}} = \text{Pourcentage d’U-235} \times \text{Masse totale} \]
Données :
- \(\text{Pourcentage d’U-235} = 5\%\)
- \(\text{Masse totale} = 47040,83 \, \text{g}\)
Calcul :
\[ Masse_{\text{U-235}} = 5\% \times 47040,83 \, \text{g} \] \[ Masse_{\text{U-235}} = 2352,04 \, \text{g} \]
Conclusion
La masse totale d’uranium enrichi nécessaire pour atteindre la masse critique est de 47040,83 g, dont 2352,04 g d’uranium-235.
Cette quantité d’uranium-235 est suffisante pour maintenir une réaction en chaîne autosuffisante dans un réacteur de recherche.
Calcul de la Masse Critique d’Uranium-235
D’autres exercices de chimie nucléaire:





0 commentaires